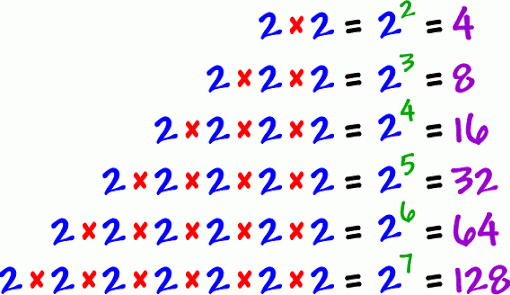Site voltado à divulgação científica, aulas e atualidades
Matemática & Afins
Matemática & Afins
Site voltado à divulgação científica, aulas e atualidades
Derivadas Matemática

A derivada da função exponencial natural e^x

Publicado

A função exponencial natural  geralmente representada de duas formas,

(1)   \begin{equation*} f(x) = e^{x} \end{equation*}

    \[ ou \]

(2)   \begin{equation*} f(x) = exp (x), \end{equation*}

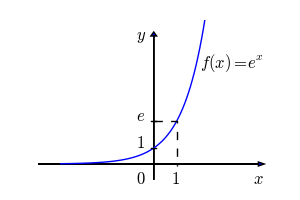
sendo esta função mais bem conhecida pelo formato apresentado em (1), o número irracional “e“, também conhecido como número de Euler, em homenagem ao matemático suíço Leonhard Euler, muitas vezes também é chamado por número de Napier ou número neperiano  que é dado pelo limite

(3)   \begin{equation*} e = \lim_{n \to \infty} (1 + \frac{1}{n})^n = 2,718281828459045 \ldots \end{equation*}

Esta função é de grande interesse científico, devido sua vasta aplicação nas ciências exatas, econômicas e inclusive biológicas, no estudo do aumento/diminuição de populações, vírus ou culturas de bactérias.

Figura 1: Definição da função natural exponencial Fonte:https://pt.wikipedia.org/wiki/Função_exponencial_natural

Imaginemos, que, caso queira se fazer a projeção de como evolui o número de pessoas contaminadas por um determinado vírus de gripe ou mesmo um hipotético vírus do “apocalipse zumbi” em função do tempo, pesquisadores deverão fazer uso de uma função matemática  que pode ser representada de maneira parecida, com o que foi apresentado em (1). Mas as aplicações da função exponencial natural vão muito além da contagem de zumbis, sendo amplamente utilizada, na economia, na estatística, no decaimento radioativo de elementos físseis, em equações de ondas mecânicas e eletromagnéticas já que permite-nos escrever funções trigonométricas de uma maneira mais “simples e elegante”.

Para demonstrar a derivada de e^x, consideraremos que pode-se reescrever os limites da equação (3)  de maneira que,

    \[ n \to 0 \;\; \leftrightarrow \;\; \frac{1}{n} \to \infty, \]

sem prejuízo algum ao resultado, a expressão para a definição do número de Euler, (3), também poderá ser dada por

(4)   \begin{equation*} e = \lim_{n \to 0} (1 + n)^\frac{1}{n}. \end{equation*}

Considerando-se a definição para a derivada, dada por

(5)   \begin{equation*} \frac{d}{dx} f(x) = \lim_{\Delta x \to 0} \frac{f(x + \Delta x) - f(x)}{\Delta x}, \end{equation*}

e fazendo uso desta definição para escrever a derivada para função exponencial natural

    \[ \frac{d}{dx} e^x = \lim_{\Delta x \to 0} \frac{e^{x + \Delta x} - e^x}{\Delta x}. \]

Neste instante, devemos levar em conta uma série manobras algébricas para simplificar esta expressão, como uma primeira abordagem, coloca-se o termo e^x em evidência,

(6)   \begin{equation*} \frac{d}{dx} e^x = e^x \cdot \lim_{\Delta x \to 0} \frac {(e^{\Delta x} - 1)}{\Delta x}, \end{equation*}

lembrando-se de que esta manobra é possível devido à regra do produto de potências de mesma base, e também porque estamos tomando o limite em relação à \Delta x.

Ante à equação (6), faz-se-á necessário uma mudança de variável considerando e^{\Delta x} - 1 = u que por consequência torna \Delta x = ln(u +1), em que ln é o logaritmo natural ou logaritmo na base e, permitindo assim reescrever a expressão do limite em função de u,

    \[ \frac{d}{dx} e^x = e^x \cdot \lim_{u \to 0} \frac{u}{ln(u + 1)}, \]

a saída algebrica é passar a variável u do numerador para denominador escrevendo seu inverso

    \[ \frac{d}{dx} e^x = e^x \cdot \lim_{u \to 0} \frac{1}{\frac{1}{u} ln(u +1)}, \]

o inverso de u pode agora ser passado para o expoente do argumento do logaritmo,

(7)   \begin{equation*} \frac{d}{dx} e^x = e^x \cdot \lim_{u \to 0} \frac{1}{ln(u + 1)^\frac{1}{u}}, \end{equation*}

além de mais compacta, deve-se confrontar aqui a equação (7) com a definição para o número de Euler dada em (4), consequentemente obtendo-se

    \[ \frac{d}{dx} e^x = e^x \cdot \frac{1}{ln(e)} = e^x \cdot 1. \]

Dessa forma, podemos afirmar que derivada da função exponencial natural, e^x, é dada por ela mesma,

(8)   \begin{equation*} \boxed{ \frac{d}{dx} e^x = e^x }, \end{equation*}

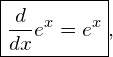
revelando, assim, o quanto essa função é impressionante, pois o valor da inclinação de sua reta tangente será sempre igual à sua altura. Imaginemos uma escadaria cuja a altura em ponto qualquer seja dado pela função natural exponencial e um atleta com a “triste” tarefa de subir tal escadaria correndo

Figura 2: Escada exponencial Fonte:https://www.dreamstime.com

No início, esta tarefa não seria tão árdua, mas com o passar das alturas, o  esforço do atleta será cada vez maior . À   medida que ele sobe, a inclinação desta escadaria será sempre igual à altura do degrau em que ele se encontra. Enfim, torna-se impossível mesmo para um atleta subir uma escada como essa chegar ao topo, caso ela seja muito alta.

 

Autor: Prof. Fábio Matos

“Aulas Particulares de Calculo, Física e Matemática”

(11) 97226-5689  Cel/WhatsApp

(11) 2243-7160  Fixo

email: fabio.ayreon@gmail.com

 

 

You may also like