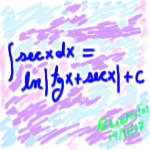![]() O determinante é a soma dos produtos dos elementos de uma fila pelos respectivos adjuntos.”
O determinante é a soma dos produtos dos elementos de uma fila pelos respectivos adjuntos.”
Antes de desenvolver o teorema, vamos recordar a definição de ![]() e
e ![]() , além de um teorema particular.
, além de um teorema particular.
![]() Chama-se Determinante Menor relativo a um elemento da matriz quadrada, o determinante que se obtém, suprimindo a lina e a coluna que se cruzam no elemento considerado.
Chama-se Determinante Menor relativo a um elemento da matriz quadrada, o determinante que se obtém, suprimindo a lina e a coluna que se cruzam no elemento considerado.
![]() O menor (Determinante) do elemento 7 no Determinante
O menor (Determinante) do elemento 7 no Determinante
![Rendered by QuickLaTeX.com \[ \Delta = \left| \begin{array}{cccc} 2 & 3 & 4 & \color{red}{5} \\ 4 & -1 & 2 & \color{red}{1} \\ \color{red}{5} & \color{red}{-3} & \color{red}{4} & \colorbox{red}{ \color{white}{ 7}} \\ 2 & 5 & 4 & \color{red}{1} \end{array} \right|, \; \acute{e} \;\;\; \delta = \left| \begin{array}{ccc} 2 & 3 & 4 \\ 4 & -1 & 2 \\ 2 & 5 & 4 \end{array} \right|. \]](https://matematicaeafins.com.br/wp-content/ql-cache/quicklatex.com-2e7ad1cf0352f854ec2407a80ebef972_l3.png)
![]() O adjunto de um elemento é o determinante menor desse elemento a que se atribui um sinal dado pela potência
O adjunto de um elemento é o determinante menor desse elemento a que se atribui um sinal dado pela potência ![]() onde
onde ![]() e
e ![]() são, respectivamente, a linha e a coluna a qual pertence o elemento considerado.
são, respectivamente, a linha e a coluna a qual pertence o elemento considerado.
Se representarmos por ![]() o adjunto do elemento considerado, temos para o adjunto do elemento 7 no determinante acima:
o adjunto do elemento considerado, temos para o adjunto do elemento 7 no determinante acima:
![Rendered by QuickLaTeX.com \[ A_{ij} = A_{34} = \left(-1 \right)^{3+4} \cdot \left| \begin{array}{ccc} 2 & 3 & 4 \\ 4 & -1 & 2 \\ 2 & 5 & 4 \end{array} \right|. \]](https://matematicaeafins.com.br/wp-content/ql-cache/quicklatex.com-84460716fbc1b5d1f6a2efa834676bf0_l3.png)
![]() Quando os elementos de uma fila são nulos, exceto um dos elementos, o determinante é igual ao produto do elemento não nulo pelo seu adjunto.
Quando os elementos de uma fila são nulos, exceto um dos elementos, o determinante é igual ao produto do elemento não nulo pelo seu adjunto.
![]() Supor que a fina de elementos nulos exceto um é a primeira e o elemento não nulo o primeiro
Supor que a fina de elementos nulos exceto um é a primeira e o elemento não nulo o primeiro
![Rendered by QuickLaTeX.com \[ \Delta = \left| \begin{array}{cccccc} a_{11} & 0 & 0 & 0 & \cdots & 0 \\ a_{21} & a_{22} & a_{23} & a_{24} & \cdots & a_{2n} \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & a_{n3} & a_{n4} & \cdots & a_{nn} \end{array} \right| \]](https://matematicaeafins.com.br/wp-content/ql-cache/quicklatex.com-aee95b86062fb552281ff9dcfa14b6ac_l3.png)
Por definição, todos os termos (parcelas) do desenvolvimento do determinante contém um elemento da primeira linha; Que se não for o primeiro elemento, a parcela é nula.
Assim, o determinante se reduz às parcelas que contém ![]() e como, obviamente, por definição de determinante, essas parcelas não terão nenhum outro elemento da primeira linha ou coluna, conclui-se que, se colocarmos
e como, obviamente, por definição de determinante, essas parcelas não terão nenhum outro elemento da primeira linha ou coluna, conclui-se que, se colocarmos ![]() em evidência, o outro fator será formado pelos elementos abaixo
em evidência, o outro fator será formado pelos elementos abaixo
![Rendered by QuickLaTeX.com \[ \delta = \left| \begin{array} {cccc} a_{22} & a_{23} & \cdots & a_{2n} \\ a_{32} & a_{33} & \cdots & a_{3n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n2} & a_{n3} & \cdots & a_{nn} \\ \end{array} \right|, \]](https://matematicaeafins.com.br/wp-content/ql-cache/quicklatex.com-fb1ea3751a0d3dd0463bc8ade92c2ad3_l3.png)
que é justamente em valor absoluto e sinal, o adjunto de ![]() , pois
, pois
![]()
![]() A fila dos elementos nulos exceto um (elemento) qualquer. Suponhamos nula a linha de ordem
A fila dos elementos nulos exceto um (elemento) qualquer. Suponhamos nula a linha de ordem ![]() e
e ![]() o elemento não nulo.
o elemento não nulo.
![Rendered by QuickLaTeX.com \[ \Delta = \left| \begin{array}{cccccc} a_{11} & a_{12} & \cdots & a_{1j} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2j} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & a_{kj} & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nj} & \cdots & a_{nn} \end{array} \right| \]](https://matematicaeafins.com.br/wp-content/ql-cache/quicklatex.com-84277e52f897a6cd18a7e880363c974e_l3.png)
O que podemos fazer é deslocar para o primeiro lugar o elemento ![]() efetuando
efetuando ![]() efetuando
efetuando ![]() trocas sucessivas de linhas e
trocas sucessivas de linhas e ![]() trocas sucessivas de colunas, lembrar que a cada troca de filas paralelas o determinante troca de sinal , isto é, fica multiplicado por
trocas sucessivas de colunas, lembrar que a cada troca de filas paralelas o determinante troca de sinal , isto é, fica multiplicado por ![]() .
.
Assim, o determinante ficará multiplicado por ![]() ou
ou ![]() é o mesmo, pois
é o mesmo, pois ![]() e
e ![]() são da mesma paridade.
são da mesma paridade.
Desta maneira, podemos escrever:
![Rendered by QuickLaTeX.com \[ \Delta = (-1)^{k+j} \left| \begin{array} {cccc} a_{kj} & 0 & \cdots & 0 \\ a_{1j} & a_{12} & \cdots & a_{1n} \\ a_{2j} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{nj} & a_{n2} & \cdots & a_{nn} \end{array} \right| \]](https://matematicaeafins.com.br/wp-content/ql-cache/quicklatex.com-82cb6542ad9c71ba6124be5e39df5480_l3.png)
Isto é![]() ou seja,
ou seja,
![]()
![]() Um Determinante Geral de ordem
Um Determinante Geral de ordem ![]() possui
possui ![]() parcelas ou termos. Em cada parcela figurará
parcelas ou termos. Em cada parcela figurará ![]() elementos, mas nunca dois elementos de uma mesma linha ou coluna e que, portanto, haverá
elementos, mas nunca dois elementos de uma mesma linha ou coluna e que, portanto, haverá ![]() parcelas contendo um único elemento de uma determinada linha
parcelas contendo um único elemento de uma determinada linha ![]() .
.
De acordo com o teorema anterior ![]()
![]() , onde,
, onde,
![]()
Os coeficientes C são adjuntos dos respectivos elementos da Linha ![]() , o que demonstra o teorema.
, o que demonstra o teorema.

Autor: Prof. Marcello Carlos,
licenciado em Matemática pela UnG
“Aulas Particulares de Calculo, Física e Matemática”
(11) 97226-5689 Cel/WhatsApp
(11) 2243-7160 Fixo
email: fabio.ayreon@gmail.com