Site voltado à divulgação científica, aulas e atualidades
Matemática & Afins
Matemática & Afins
Site voltado à divulgação científica, aulas e atualidades
Geometria espacial Matemática

Superfícies poliédricas abertas e fechadas

Publicado

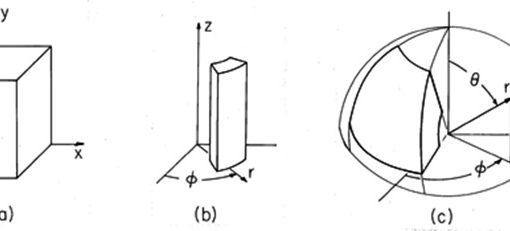
Superfície poliédrica convexa aberta

 

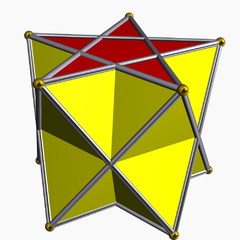
Figura 1: Superfície poliédrica aberta – Antiprisma pentagramico uniforme. Fonte:https://en.wikipedia.org/wiki/Pentagrammic_antiprism

Lema.  Em toda superfície poliédrica convexa aberta, o número de arestas aumentado de 1  é igual ao número de faces mais o número de vértices.

Seja A, F e V o número  de arestas, faces e vértices, respectivamente, vamos mostrar que A+1 = V + F, isto é,

(1)   \begin{equation*} V-A+F=1. \end{equation*}

Evidentemente a igualdade (1) é satisfeita para uma superfície poliédrica de uma face, no caso, um polígono plano.

Então,

    \[A = V, F = 1 \;\; \longrightarrow \;\; A+1 = V+F \;\; ou \;\; V-A+F=1. \]

Decorre que, sendo (1) verdadeira para uma face, vamos mostrar por recorrência ou indução que o Lema é verdadeiro para toda superfície poliédrica aberta, isto é, se vale para F=1, vale para F>1, ou em outras palavras, se o Lema é verdadeiro para uma superfície de n faces, então o será para n+1 faces.

Sejam F', V' e A', respectivamente, as faces, vértices e arestas da superfície de n+1 faces. Temos que,

(2)   \begin{equation*} F' = F + 1. \end{equation*}

Supondo que a face acrescentada possua l lados dos quais c coincidam com as faces da superfície poliédrica de n faces, concluímos que o número de arestas acrescentadas à superfície de n faces é l - c, e portanto,

(3)   \begin{equation*} A' = A + l - c. \end{equation*}

O número de vértices coincidentes da face acrescentada, é igual ao número de arestas coincidentes mais um, isto é, c + 1.

Então, o número de vértices acrescentados à superfície poliédrica primitiva (n faces) será l - (c + 1) e portanto, temos:

(4)   \begin{equation*} V' = V + l - c - 1. \end{equation*}

Somando (2) com (4) e subtraindo (3), obtemos

    \[ F' + V' - A' = F + 1 + V + l - c - A - l + c\]

 

    \[ \therefore \;\; F' + V' - A' = F + V - A.\]

Como

    \[F +V - A = 1,\]

por hipótese, então,

    \[F' + V' - A = 1,\]

    \[ ou \]

    \[ A' + 1 = V' + F'.\]

Pelo fato de (1) ser verificada, o Lema é verdadeiro para um número qualquer finito de faces.

 

Superfície poliédrica convexa fechada

 

Teorema (Euler). Em todo poliedro convexo, o número de Arestas acrescido de 2 é igual à soma do número de Faces com o número de Vértices.

 

Figura 2: Superfície poliédrica fechada, prisma hexagonal – Fonte:https://en.wikipedia.org/wiki/Hexagonal_prism

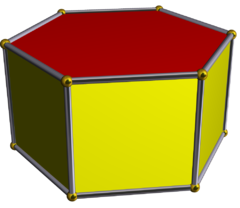
Vamos mostrar que,

    \[A+2 = V+F,\]

    \[ ou\]

    \[V-A+F=2,\]

para um poliedro com superfície poliédrica fechada.

Suprimindo uma face do poliedro convexo, obtemos, obviamente, uma superfície poliédrica aberta convexa cujo número de Arestas e de Vértices é o mesmo do poliedro.

De acordo com o lema, para uma superfície poliédrica aberta conforme supracitado

    \[A+1 = V+F.\]

Aumentando uma face, fechando a superfície, temos o poliedro nas condições,

    \[A = A', \;\; V = V' \;\; e\;\; F' = F+1,\]

e portanto

    \[A'+1 = V'+F'-1\]

que consequentemente implica em

    \[ \boxed{ A'+2 = V'+F'.} \]

 

Autor: Prof. Marcello Carlos,

licenciado em Matemática pela UnG

 

 

 

 

 

Contato para  “Aulas Particulares de Calculo, Física e Matemática”

(11) 97226-5689  Cel/WhatsApp

(11) 2243-7160  Fixo

email: fabio.ayreon@gmail.com

 

 

You may also like