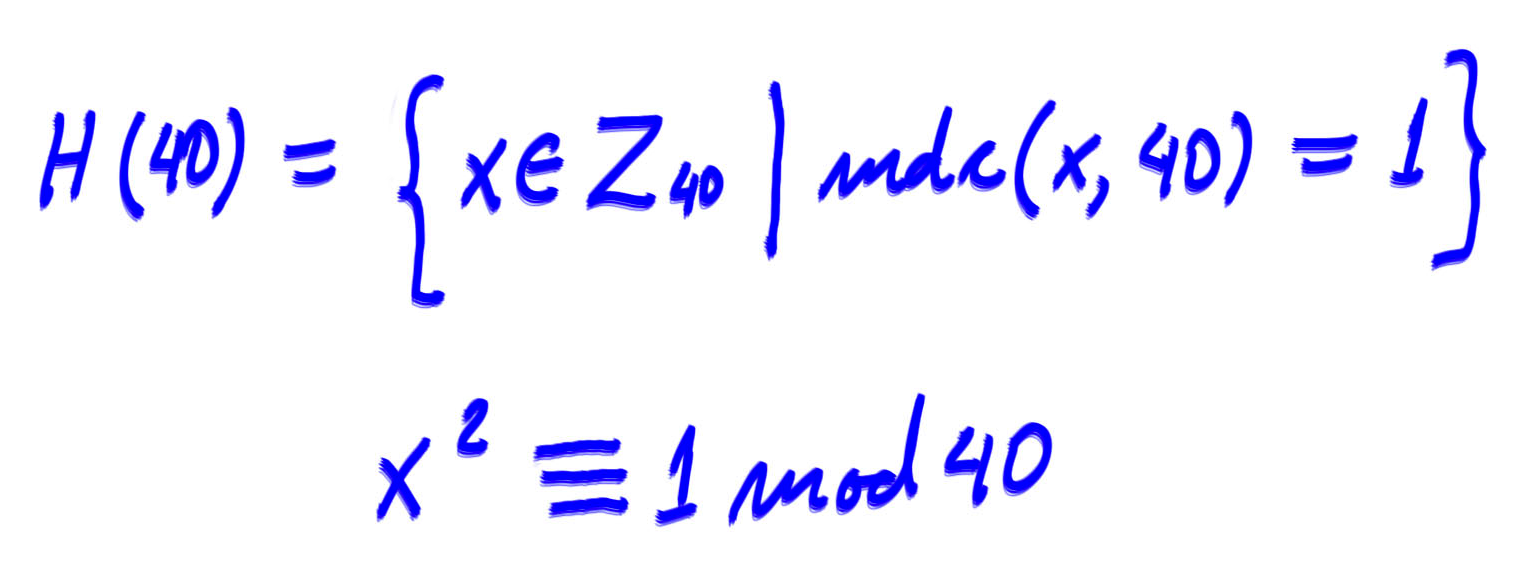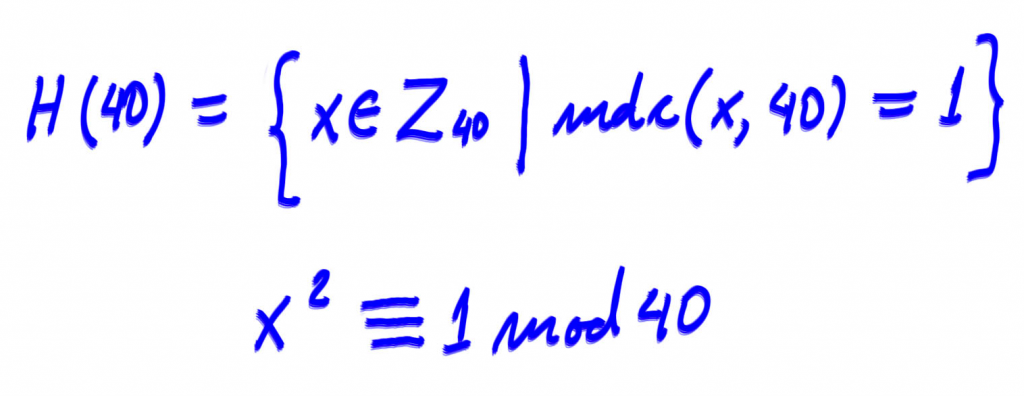
Resposta:
Existem duas classes de isomorfismo para grupos de ordem 4:
Ou um grupo desordem quatro é isomorfico para o grupo cíclico 
ou um grupo de ordem quatro é isomorfico para o grupo Quatro de Klein. Lembrando que o grupo Quatro de Klein é não cíclico desde que todo elemento elevado ao quadrado resulta na identidade. Isso significa que um grupo que não possui elemento de ordem quatro não pode ser cíclico.
Assim, se existe um subgrupo não cíclico de ordem em
![\[ H(40)\,=\, \{x \,\in\, Z_{40} \, | \, mdc(x, 40) \,=\, 1 \} \]](https://matematicaeafins.com.br/wp-content/ql-cache/quicklatex.com-5f2697ce302e7c19160eeb345508d833_l3.png "Rendered by QuickLaTeX.com")
então ele deve ser isomorfico para o grupo Quatro de Klein. Então ele deve possuir o elemento identidade e deve possuir três elementos cujo quadrado é a própria identidade.
Em outras palavras, queremos encontrar os elementos 
tais que 
é o elemento identidade em 
.
Lembrando que a multiplicação é reduzida a 
no grupo 
. Dessa maneira, argumentando que de ser o elemento identidade em é equivalente a argumentar que
![\[ x^2\,\equiv\, 1\,mod(40) . \]](https://matematicaeafins.com.br/wp-content/ql-cache/quicklatex.com-2eb0cf5f2f4e3a38b01f60b03a9c8f58_l3.png "Rendered by QuickLaTeX.com")
Para encontrar tais valores para 
, começaremos procurando por números que sejam congruentes a 
e verificar se eles são realmente quadrados perfeitos.
é um quadrado perfeito então deve ser nosso subgrupo não cíclico de ordem quatro.- não é um quadrado perfeito.
- é um quadrado perfeito então deve ser nosso subgrupo não cíclico de ordem quatro.
- é um quadrado perfeito então deve ser nosso subgrupo não cíclico de ordem quatro.
- é um quadrado perfeito então deve ser nosso subgrupo não cíclico de ordem quatro.
é um quadrado perfeito então 
deve ser nosso subgrupo não cíclico de ordem quatro.
não é um quadrado perfeito.
é um quadrado perfeito então 
deve ser nosso subgrupo não cíclico de ordem quatro.
é um quadrado perfeito então 
deve ser nosso subgrupo não cíclico de ordem quatro.
é um quadrado perfeito então 
deve ser nosso subgrupo não cíclico de ordem quatro.Assim, nós temos o subgrupo não cíclico 
com a tabela de multiplicação que segue:
![\[ \begin{tabular}{c|c c c c} \star & \textbf{1} & \textbf{9} & \textbf{11} & \textbf{19} \\ \hline \textbf{1} & 1 & 9 & 11 & 19 \\ \textbf{9} & 9 & 1 & 19 & 11 \\ \textbf{11} & 11 & 19 & 1 & 9 \\ \textbf{19} & 19 & 11 & 9 & 1 \\ \end{tabular} \]](https://matematicaeafins.com.br/wp-content/ql-cache/quicklatex.com-2fa9891e8413210e441f97d3791bd7dd_l3.png "Rendered by QuickLaTeX.com")
Dessa forma, concluimos que o grupo é isomorfico para o grupo Quatro de Klein.
Autor: Prof. Fábio Matos
“Aulas Particulares de Calculo, Física e Matemática”
(11) 97226-5689 Cel/WhatsApp
(11) 2243-7160 Fixo
email: fabio.ayreon@gmail.com
