Problema aplicado no exame nacional de matemática e estatística do governo Neozelandês gera polêmica e ganha destaque na mídia internacional com repercussão nos principais jornais da Austrália, Reino Unido e Estados Unidos.
O exame ocorreu em novembro de 2017, e uma das questões que ganhou notoriedade faz parte da prova de 
que é aplicada a estudantes de 15 anos de idade. O problema em si não é impossível, mas o que chama a atenção é o seu grau de dificuldade já que a sua solução requer conhecimento e muito amadurecimento em geometria. Algo que é raro para esta idade.
O problema da pipa
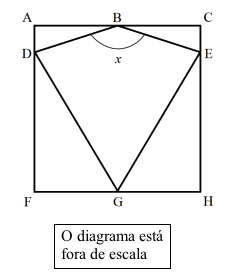
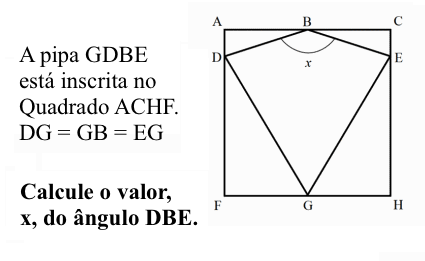
A pipa GDBE está inscrita no quadrado ACHF. Considere 
.
Calcule a medida, 
, do ângulo 
.
Justifique sua resposta com clareza e argumentos geométricos.
Solução:
Levando-se em consideração que as medidas , e que 
é uma pipa, pode-se afirmar que 
.
Consequentemente temos que os triângulos 
e 
são côngruos pelo critério 
.
Desenhando-se as diagonais 
e 
para encontrar o ponto de intersecção 
,
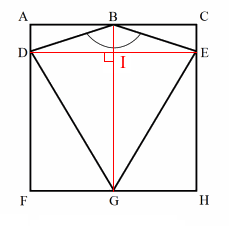
temos que, é perpendicular a no ponto , de maneira que 
.
Lembrando que 
, pode-se concluir o seguinte:
![\[ DG=GE=BG=2(DI) = 2(IE). \]](https://matematicaeafins.com.br/wp-content/ql-cache/quicklatex.com-c70b5674be9c80e7aab039f7e6174474_l3.png "Rendered by QuickLaTeX.com")
Dessa maneira os triângulos retângulos 
e 
têm ângulos cujos valores são 
, 
e 
. Sabe-se assim que, os ângulos 
, ou seja,
![\[ D\hat{G}E = D\hat{G}B + E\hat{G}B = 60^{o}. \]](https://matematicaeafins.com.br/wp-content/ql-cache/quicklatex.com-489a5699750754bd92e341bc24e3ec26_l3.png "Rendered by QuickLaTeX.com")
Os triângulos 
e 
são isósceles e congruentes pelo critério 
, que nos leva aos resultados,
![\[ B\hat{D}G \equiv B\hat{E}G \equiv \frac{D\hat{B}E}{2} = \frac{x}{2}. \]](https://matematicaeafins.com.br/wp-content/ql-cache/quicklatex.com-a2d40ec6e9455a7fc3ca0f4145420f12_l3.png "Rendered by QuickLaTeX.com")
Assim, levando-se em conta que a soma dos ângulos internos de um quadrilátero é igual a 
, escreve-se a seguinte relação para os ângulos internos da pipa ,
![\[ med(D \hat{B} E) +med(B \hat{E} G) + med(E \hat{G} D) + med(G \hat{D} B) = 360^{o} \]](https://matematicaeafins.com.br/wp-content/ql-cache/quicklatex.com-d722fe58496fbe9579131ff7d03aa44c_l3.png "Rendered by QuickLaTeX.com")
![\[ x+\frac{x}{2} + 60^o + \frac{x}{2} = 360^o \]](https://matematicaeafins.com.br/wp-content/ql-cache/quicklatex.com-1c8f914efebc7f178bfb3e08a1825d37_l3.png "Rendered by QuickLaTeX.com")
![\[ 2x = 300^o \]](https://matematicaeafins.com.br/wp-content/ql-cache/quicklatex.com-5fb23b31dee955f0fae3746063c961ab_l3.png "Rendered by QuickLaTeX.com")
![\[ \boxed{ x = 150^o}. \]](https://matematicaeafins.com.br/wp-content/ql-cache/quicklatex.com-8be67b471e05d6a841895286ecebf8a7_l3.png "Rendered by QuickLaTeX.com")
Autor: Prof. Fábio Matos
“Aulas Particulares de Calculo, Física e Matemática”
(11) 97226-5689 Cel/WhatsApp
(11) 2243-7160 Fixo
email: fabio.ayreon@gmail.com
