Resposta:
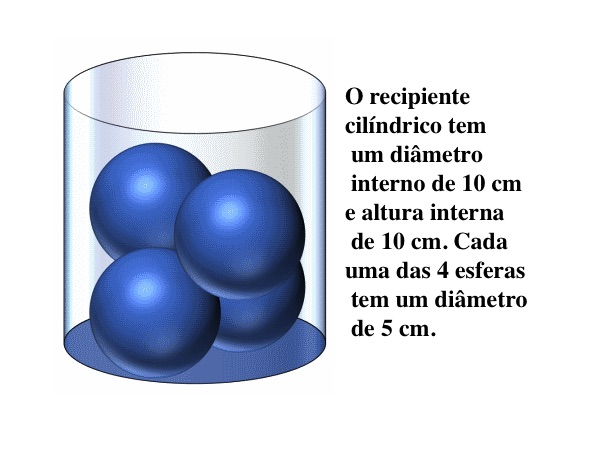
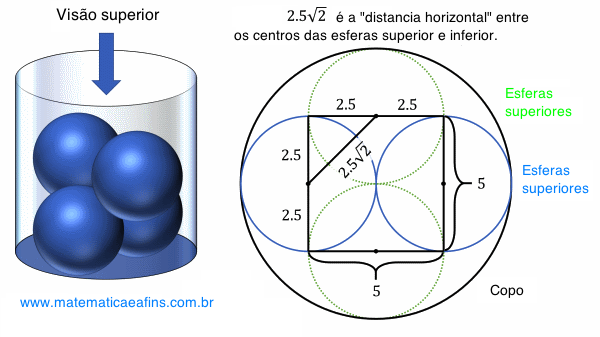
Uma maneira de abordar o problema é considerar a visão de cima. Veremos que o copo como um circulo. Dentro estão as bordas circulares para as duas esferas de cima, que se tangenciam e tangenciam o copo. As duas esferas do fundo estão rotacionadas em 90 graus em relação às duas de cima – assim, os dois círculos são tangentes entre si e ao copo.
O diametro de cada esfera é 
, então cada raio vale 
. Nos podemos encontrar a distancia horizontal entre os centros das esferas do topo e do fundo do copo que é 
, já que cada lado do triângulo retângulo formado mede .
Nos podemos considerar um triângulo retângulos com as seguintes características.
Seja a hipotenusa o seguimento de reta conectando os centros das esferas superior e inferior. Essa hipotenusa terá um comprimento de 
, pois os círculos são tangentes entre si.
Um dos catetos do triângulo retângulo é a medida horizontal, , que já calculamos.
O outro cateto será dado a distância vertical, entre os centros das esferas superior e inferior. Como este triângulo retângulo é isósceles, então a distância vertical também será .
Agora podemos resolver a altura do topo da esfera superior. Ela será dada pelo comprimento de dois raios mais a distância vertical entre os centros, que é 
Então distância vertical será dada por 
.
Para calcular o volume de água necessário para cobrir as esferas superiores vamos considerar o volume do cilindro que alcança as esferas superiores, e então subtrair o volume das quatro esferas dadas.
O cilindro tem volume
![\[ V_C\,=\,\pi\cdot R^{2} \cdot h, \]](https://matematicaeafins.com.br/wp-content/ql-cache/quicklatex.com-41cd8a6c4cea708a17c73e7aeb4dc875_l3.png "Rendered by QuickLaTeX.com")
sendo que 
e 
.
Cada esfera tem um volume
![\[ V_E\,=\,\frac{4}{3}\pi \cdot r^{3}, \]](https://matematicaeafins.com.br/wp-content/ql-cache/quicklatex.com-ce718a6d6259ea53ae6afcc29c85f320_l3.png "Rendered by QuickLaTeX.com")
sendo 
.
Então, o volume da água será
![\[ \begin{array}{l} V_{agua}\,=\,V_C\,-\,4 \cdot V_E \\ \\ V_{agua}\,=\,\pi\cdot R^{2} \cdot h\,-\,4\cdot\frac{4}{3}\pi \cdot r^{3} \\ \\ V_{agua}\,=\, \pi 5^{2}(5\,+\,2,5\sqrt{2})\, - \,\frac{16}{3}\pi (2,5)^3 \\ \\ V_{agua}\,=\, \pi 5^{2}(5\, + \, \frac{5}{2}\sqrt{2})\, - \, \frac{16}{3} \pi \left( \frac{5}{2} \right)^{3} \\ \\ V_{agua}\,=\, 125 \pi \left (1\, + \, \frac{\sqrt{2}}{2} \, - \, \frac{2}{3} \right) \\ \\ \\ \fbox{V_{agua}\,=\, \frac{125 \pi}{6} \left(2 \,+\, 3\sqrt{2} \right)\,cm^{3}}. \end{array} \]](https://matematicaeafins.com.br/wp-content/ql-cache/quicklatex.com-acb1d0deffcc9be6a413472116d960c4_l3.png "Rendered by QuickLaTeX.com")
Autor: Prof. Fábio Matos
“Aulas Particulares de Calculo, Física e Matemática”
(11) 97226-5689 Cel/WhatsApp
(11) 2243-7160 Fixo
email: fabio.ayreon@gmail.com
