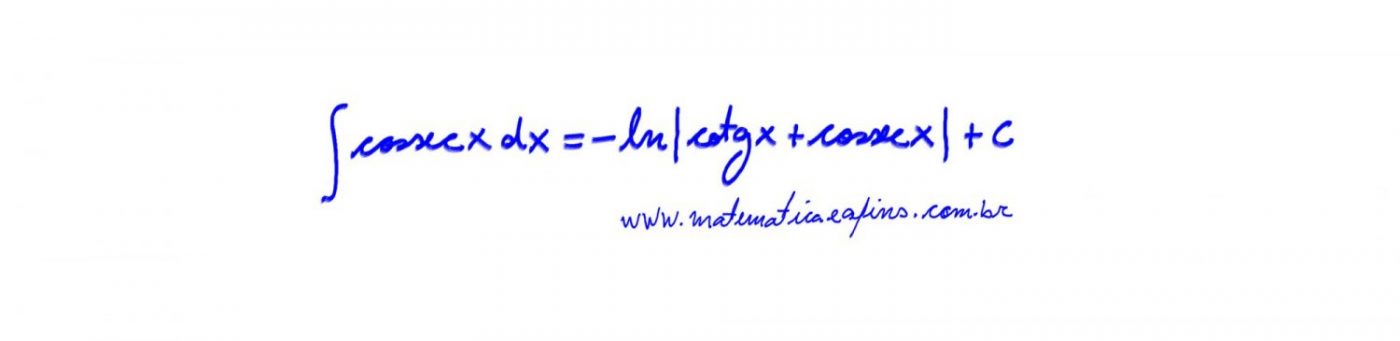Discussão da integral
(1) 
A solução para a integral acima (1) não é obvia, a estratégia a ser utilizada, será multiplicar e dividir esta expressão por 
,
(2) 
A partir daqui, o caminho é fazer uma substituição de variáveis, no caso, deve-se considerar nesta substituição
(3) 
cuja derivada em relação à variável 
é dada por
(4) 
que em seguida dando uma leve “melhorada” por meio de fatoração, a expressão (4) torna-se
(5) 
Considerando-se os resultados obtidos nas equações (3) e (5) substitui-mo-las respectivamente nos numerador e denominador da equação (2) de maneira que, obtêm-se uma integral mais enxuta dada por
(6) 
cujo consequente resultado do lado direito da equação é
(7) 
É claro que não podemos devolver o resultado em função de 
. A substituição feita utilizando a variável , foi apenas um artifício para tornar mais palatável a resolução da integral (1). Desta maneira, faz-se-á necessário substituir a expressão (3) em (7) para obter-se o resultado
(8) 
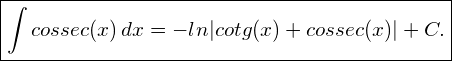
Autor: Prof. Fábio Matos
“Aulas Particulares de Calculo, Física e Matemática”
(11) 97226-5689 Cel/WhatsApp
(11) 2243-7160 Fixo
email: fabio.ayreon@gmail.com
