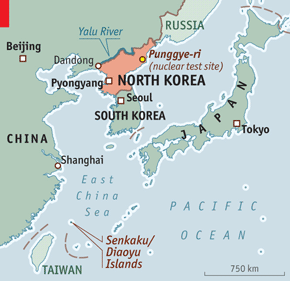
No dia 3 de setembro de 2017, o governo japonês, após analisar os dados de sismógrafos, anunciou que a Coreia do Norte havia realizado um teste nuclear em uma instalação subterrânea em Punggye-ri, o qual gerou um sismo de magnitude de 6.3, o maior dos últimos cinco testes já realizados pela Coreia do Norte. Este teste foi confirmado horas mais tarde pelo Governo de Pyongyang, que afirmou se tratar de uma bomba de Hidrogênio, parecendo pouco provável, mesmo assim, a notícia alarmou o mundo trazendo mais instabilidade para os países da região que vislumbram no horizonte a possibilidade de um conflito de dimensões catastróficas.
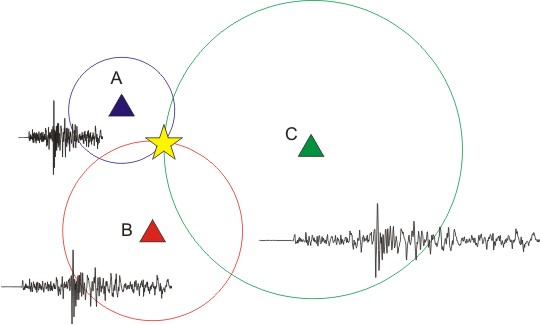
Ante esta situação, é interessante notar a rapidez com que o governo japonês anuncia a realização dos testes nucleares coreanos, seis até então, afirmando de maneira categórica o local de realização dos mesmos, como isso é possível, apenas com o uso de sismógrafos já que a distância entre Pyongyang e Tóquio é de cerca de 1300 km tendo inclusive o Mar do Japão separando-os.
Para determinar o local da explosão nuclear, ou mesmo, o epicentro de um terremoto, consideremos que ![]() é o ponto de origem do sismo (epicentro) ou ponto de realização do teste nuclear em relação a um referencial qualquer dado em coordenadas cartesianas.
é o ponto de origem do sismo (epicentro) ou ponto de realização do teste nuclear em relação a um referencial qualquer dado em coordenadas cartesianas.
Os pontos ![]() ,
, ![]() e
e ![]() representam respectivamente as coordenadas de localização de três sismógrafos hipotéticos
representam respectivamente as coordenadas de localização de três sismógrafos hipotéticos ![]() ,
, ![]() e
e ![]() localizados em relação a um referencial qualquer em coordenadas cartesianas. Sim, são necessários pelo menos três sismógrafos para determinar o epicentro, já que cada sismógrafo permite medir “apenas” magnitude e a distância do ponto de origem do tremor, caso queiramos a profundidade do epicentro deveríamos levar em conta, pelo menos, os dados de quatro sismógrafos.
localizados em relação a um referencial qualquer em coordenadas cartesianas. Sim, são necessários pelo menos três sismógrafos para determinar o epicentro, já que cada sismógrafo permite medir “apenas” magnitude e a distância do ponto de origem do tremor, caso queiramos a profundidade do epicentro deveríamos levar em conta, pelo menos, os dados de quatro sismógrafos.
Na leitura do sismógrafo deve ser tomado o intervalo de tempo ![]() ocorrido entre as ondas Primária P e Secundária S, este intervalo de tempo
ocorrido entre as ondas Primária P e Secundária S, este intervalo de tempo ![]() , é o mesmo tempo que onda leva de seu epicentro até o sismógrafo.
, é o mesmo tempo que onda leva de seu epicentro até o sismógrafo.
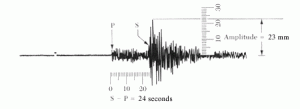
O valor da velocidade de deslocamento ![]() da onda sísmica, geralmente é um dado experimental conhecido e que varia em função da densidade e da rigidez dos materiais que compõem o meio pelo qual essas ondas se deslocam. No caso das ondas Primárias P os valores são de
da onda sísmica, geralmente é um dado experimental conhecido e que varia em função da densidade e da rigidez dos materiais que compõem o meio pelo qual essas ondas se deslocam. No caso das ondas Primárias P os valores são de ![]() para a crosta continental e
para a crosta continental e ![]() para a crosta oceânica, já para as ondas secundárias S os valores são de
para a crosta oceânica, já para as ondas secundárias S os valores são de ![]() para a crosta continental e
para a crosta continental e ![]() para a crosta oceânica.
para a crosta oceânica.
Tendo-se a velocidade de deslocamento da onda sísmica e os tempos deslocamento (![]() ) da onda sísmica desde o epicentro até cada um dos sismógrafos (A, B e C respectivamente), podemos afirmar que as distâncias de entre o epicentro e cada um dos sismógrafos serão dadas por
) da onda sísmica desde o epicentro até cada um dos sismógrafos (A, B e C respectivamente), podemos afirmar que as distâncias de entre o epicentro e cada um dos sismógrafos serão dadas por
(1) 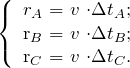
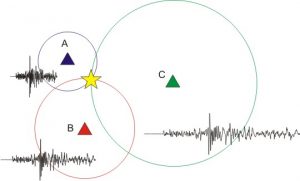
Com o conhecimento das distâncias entre os três sismógrafos ao epicentro, vamos determinar as coordenadas ![]() do epicentro fazendo uso de um sistema com três equações da circunferência, que têm como como centro os sismógrafos
do epicentro fazendo uso de um sistema com três equações da circunferência, que têm como como centro os sismógrafos ![]() ,
, ![]() e
e ![]() , tendo em vista que a solução deste sistema é exatamente o ponto de encontro das três circunferências, este método é também chamado de triangulação.
, tendo em vista que a solução deste sistema é exatamente o ponto de encontro das três circunferências, este método é também chamado de triangulação.
(2) ![]()
(3) ![]()
(4) ![]()
Expandindo-se agora os produtos notáveis e passando as constantes para o segundo membro das equações
(5) ![]()
(6) ![]()
(7) ![]()
Utilizando-se a equação (5) para reescrever as equações (6) e (7) e em seguida escalonando-as obtêm-se
(8) ![Rendered by QuickLaTeX.com \begin{equation*} \left \{ \begin{align*} 2x(x_A - x_B) + &2y(y_A - y_B) = (r_B^2 - x_B^2 - y_B^2) - (r_A^2 - x_A^2 - y_A^2)\\ \\&2y[(y_A - y_C)(x_A - x_B) - (y_A - y_B)(x_A - x_C)] = (x_A - x_B)[(r_C^2 - x_C^2 - y_C^2) - (r_A^2 - x_A^2 - y_A^2)] -\\ &- (x_A - x_C)[(r_B^2 - x_B^2 - y_B^2) - (r_A^2 - x_A^2 - y_A^2)] \end{align*} \end{equation*}](https://matematicaeafins.com.br/wp-content/ql-cache/quicklatex.com-31bd1c23bef3c9ec69110bc67639170b_l3.png)
que consequentemente pode-se resolver para ![]() e
e ![]() a expressão para as coordenadas do epicentro em função das posições dos sismógrafos
a expressão para as coordenadas do epicentro em função das posições dos sismógrafos ![]() ,
, ![]() e
e ![]() dada por
dada por
(9) ![Rendered by QuickLaTeX.com \begin{equation*} \left \{ \begin{align*} x =& \frac{(r_B^2 - x_B^2 - y_B^2) - (r_A^2 - x_A^2 - y_A^2)}{2(x_A - x_B)} - \\ &-(y_A - y_B)\frac{(x_A - x_B)(r_C^2 - x_C^2 - y_C^2 - r_A^2 + x_A^2 + y_A^2) - (x_A - x_C)(r_B^2 - x_B^2 - y_B^2 - r_A^2 + x_A^2 + y_A^2)} {2(x_A - x_B)[(y_A - y_C)(x_A - x_B) - (y_A - y_B)(x_A - x_C)] };\\ \\ y =& \frac{(x_A - x_B)(r_C^2 - x_C^2 - y_C^2 - r_A^2 + x_A^2 + y_A^2) - (x_A - x_C)(r_B^2 - x_B^2 - y_B^2 - r_A^2 + x_A^2 + y_A^2)} {2[(y_A - y_C)(x_A - x_B) - (y_A - y_B)(x_A - x_C)] }. \end{align*} \end{equation*}](https://matematicaeafins.com.br/wp-content/ql-cache/quicklatex.com-5356e19dd51988299db1a12f7327938c_l3.png)
Nota-se que esta é uma clara aplicação da equação da circunferência, neste caso um sistema com três equações, como já foi comentado, um sistema com quatro equações da esfera possibilitariam conhecer a profundidade deste epicentro já que a equação da esfera é escrita em coordenadas ![]() .
.
É interessante salientar que até o advento dos computadores, a triangulação era feita por meio de telefone/fax (único meio de integrar os sismógrafos), mapa e compasso. Hoje em dia, há uma integração maior dos dados e havendo mais de três sismógrafos envolvidos, permite-se assim uma precisão maior da localização dos epicentros dos tremores bem como a redução de algum possível erro sistemático por meio de estatística.

Autor: Prof. Fábio Matos
Contato para “Aulas Particulares de Calculo, Física e Matemática”
(11) 97226-5689 Cel/WhatsApp
(11) 2243-7160 Fixo
email: fabio.ayreon@gmail.com