Uma forma de se obter o Logaritmo Natural de um número no escopo dos Reais em condições estabelecidas, é através da identidade
(1) 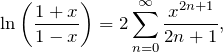
na condição ![]() .
.
Exemplo: Calcular ![]() .
.
Solução: Usando a identidade acima, isto é, a função ![]() escrita por uma série de potências, única, e em particular
escrita por uma série de potências, única, e em particular ![]() , temos:
, temos:
![]()
Daí,
![Rendered by QuickLaTeX.com \[ \ln \left( 5 \right) = 2 \cdot \sum_{n=0}^{\infty} \frac{ \left( \frac{2}{3} \right)^{2n+1}}{2n+1} \]](https://matematicaeafins.com.br/wp-content/ql-cache/quicklatex.com-cbfd624bf54f094ef9b5f3163df1b72b_l3.png)
ou seja,
![]()
E de fato para qualquer ![]()
(2) 
Podemos justificar a identidade supracitada, usando como “caminho” uma Série Geométrica de razão ![]() , tal que
, tal que ![]() .
.
Seja a série
![]()
isto é temos:
![Rendered by QuickLaTeX.com \[ \sum_{n=0}^{\infty} \frac{x^{2n+1}}{2n+1} \]](https://matematicaeafins.com.br/wp-content/ql-cache/quicklatex.com-7d5e375966cd1c708d2cbd072a6a6003_l3.png)
Derivando em relação a x:
![Rendered by QuickLaTeX.com \[ \frac{d}{dx}\, \left( \sum_{n=0}^{\infty} \frac{x^{2n+1}}{2n+1} \right) = \sum_{n=0}^{\infty} x^{2n}. \]](https://matematicaeafins.com.br/wp-content/ql-cache/quicklatex.com-67abc37e762c849644ed81de97a6146e_l3.png)
Ocorre que ![]() é uma Série Geométrica de razão
é uma Série Geométrica de razão ![]() e primeiro termo
e primeiro termo ![]() .
.
Portanto,
![Rendered by QuickLaTeX.com \[ \sum_{n=0}^{\infty} x^{2n} = \frac{1}{1-x^{2}} \; , \;\; \left|x^{2}| < 1. \]](https://matematicaeafins.com.br/wp-content/ql-cache/quicklatex.com-2214c516621bd6264988fa28bda64056_l3.png)
Vamos agora integrar a expressão ![]() , para “compensar” a derivação e encontrar uma primitiva.
, para “compensar” a derivação e encontrar uma primitiva.
(3) 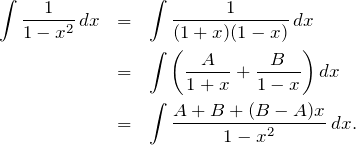
Pela identidade de polinômios
![]()
temos, portanto,
(4) 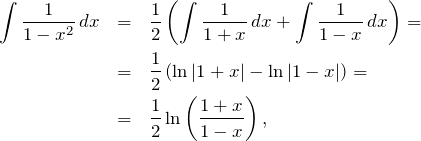
pois ![]() e
e ![]()
Fica, então, estabelecida a identidade
![Rendered by QuickLaTeX.com \[ \frac{1}{2} \ln \left( \frac{1+x}{1-x} \right) = \sum_{n=0}^{\infty} \frac{x^{2n+1}}{2n+1}, \]](https://matematicaeafins.com.br/wp-content/ql-cache/quicklatex.com-e35f71ad2f7a483191221c44fa093773_l3.png)
![Rendered by QuickLaTeX.com \[ \boxed{ \ln \left( \frac{1+x}{1-x} \right) = 2\sum_{n=0}^{\infty} \frac{x^{2n+1}}{2n+1}. } \]](https://matematicaeafins.com.br/wp-content/ql-cache/quicklatex.com-81a4f07de7c70a7fe118aea1c8b56fc6_l3.png)

Autor: Prof. Marcello Carlos,
licenciado em Matemática pela UnG
“Aulas Particulares de Calculo, Física e Matemática”
(11) 97226-5689 Cel/WhatsApp
(11) 2243-7160 Fixo
email: fabio.ayreon@gmail.com




