Por Fábio Matos
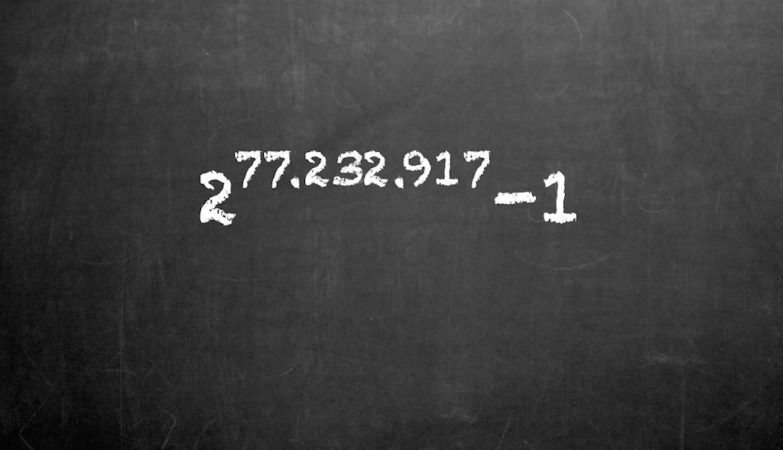
Matemáticos profissionais e amadores, que integram um projeto de pesquisa mundial – o Great Internet Mersenne Prime Search (GIMPS) – descobriram o maior número primo conhecido até hoje.
“Aulas Particulares de Calculo, Física e Matemática”
(11) 97226-5689 Cel/WhatsApp
(11) 2243-7160 Fixo
email: fabio.ayreon@gmail.com
Matemáticos que integram o Great Internet Mersenne Prime Search (GIMPS) descobriram o maior número primo conhecido até hoje: expresso na forma abreviada como 282,589,933-1, o número contém 24,862,048 dígitos, mais de um milhão e meio de dígitos maior do que o número primo do recorde anterior que foi descoberto em 2017.
Este número pertence a uma classe especial de números primos raros, denominados primos de Mersenne e é apenas o 51º primo de Mersenne já descoberto, algo que é cada vez mais difícil de encontrar.
Segundo o Sci-News, o recém-descoberto número primo foi apelidado de M82589933 e foi descoberto ao calcular dois elevado a 82,589,933, subtraindo um.
Um primo de Mersenne é um número primo da forma 2P-1. À medida que os números vão ficando maiores, os números primos – ou seja, um número divisível por 1 e por ele mesmo – tornam-se cada vez mais difíceis de serem encontrados.
Como se tornam cada vez mais distantes e como não há qualquer padrão da sua distribuição, não é possível usar um algoritmo para descobrir estes números. Aliás, até a formula para encontrar números primos Mersenne não é um método infalível, é apenas uma aproximação para os números mais prováveis.
Os primeiros primos de Mersenne são 3, 7, 31 e 127, correspondendo a P = 2, 3, 5 e 7, respetivamente. Os primos de Mersenne têm sido centrais na teoria dos números desde que foram discutidos pela primeira vez pelo matemático grego Euclides, por volta de 350 a.C..
O homem cujo nome agora ostentam, o monge francês Marin Mersenne (1588-1648), criador dessa famosa conjetura em que os valores de P gerariam um primo.
Desta forma, Euclides provou que todo o primo Mersenne gera um número perfeito – um número cujos divisores apropriados se somam ao próprio número. Por exemplo, o menor número perfeito é 6 = 1 + 2 + 3 e o segundo número perfeito é 28 = 1 + 2 + 4 + 7 + 14.
Leonhard Euler (1707-1783), um matemático suíço, provou, por sua vez, que todos os números perfeitos vêm dos primos de Mersenne. O recém-descoberto número perfeito é 282,589,932 * (282,589,933-1), um número que conta com mais de 49 milhões de dígitos.
Fonte: sci-news.com




