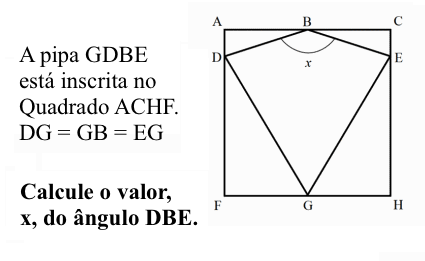
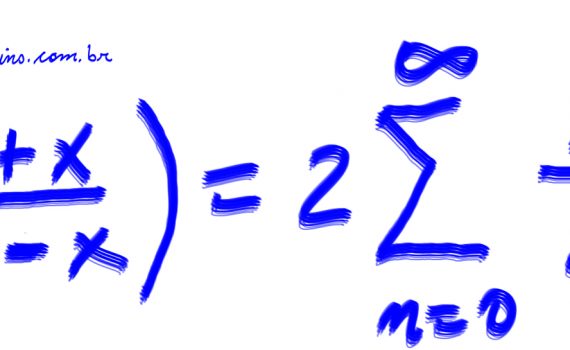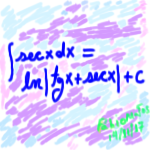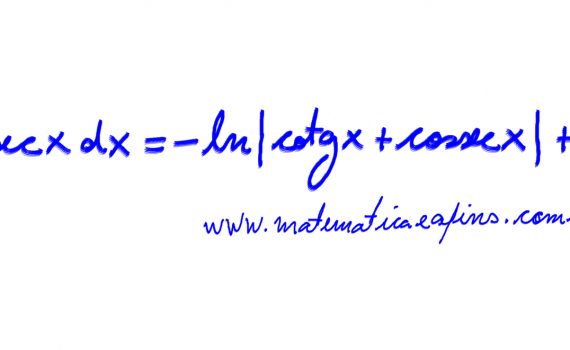Na sequência numérica o quinto termo é . O produto do primeiro com o décimo quinto termos dessa sequência é igual a (A) (B) (C) (D) (E) Solução: Considerando-se que é possível reescrever a PG alternante dada como uma série de potências de base 2, tem-se, então: Assim, o resultado […]
Matemática
OBJETIVA 2016 – Agente administrativo auxiliar – Prefeitura de Terra de Areia – RS Considerando-se as raízes das equações do grau, numerar a coluna de acordo com a e, após, assinalar a alternativa que apresenta a sequência CORRETA: (1) ambas as raízes são positivas e possuem valores diferentes. (2) ambas […]
VUNESP 2016 – Analista Programador Júnior (FUNDENESP) Em um grupo composto por 180 pessoas, há quem fala inglês, francês ou espanhol, além do português, que todos falam. Considere que x pessoas falem as quatro línguas e as seguintes informações: exatamente o dobro de x fala somente o português, o inglês […]
Regra de Três Simples Vídeo aula 1 VUNESP 2015 – Questão 21 – Concurso PM-SP Professor: Fábio Matos Direção & Produção Insight Consultoria de Marketing (11) 3294-2520 Fixo (11) 97140-9838 WhatsApp Prof. Fábio Matos “Aulas Particulares de Calculo, Física e Matemática” (11) 97226-5689 Cel/WhatsApp (11) 2243-7160 Fixo
MMC Vídeo aula 1 VUNESP 2015 – Questão 20 – Concurso PM-SP Professor: Fábio Matos Direção & Produção Insight Consultoria de Marketing (11) 3294-2520 Fixo (11) 97140-9838 WhatsApp Prof. Fábio Matos “Aulas Particulares de Calculo, Física e Matemática” (11) 97226-5689 Cel/WhatsApp (11) 2243-7160 Fixo
Frações Vídeo aula 1 Transformando de decimal para fração VUNESP 2015 – Questão 19 – Concurso PM-SP Professor: Fábio Matos Direção & Produção Insight Consultoria de Marketing (11) 3294-2520 Fixo (11) 97140-9838 WhatsApp Prof. Fábio Matos “Aulas Particulares de Calculo, Física e Matemática” (11) 97226-5689 Cel/WhatsApp (11) 2243-7160 Fixo
(VUNESP – TCE/SP – 2017 – Agente da Fiscalização) Considere verdadeiras as afirmações I, II, III e falsa a afirmação IV. I. Se como, então não sinto fome. II. Não sinto fome ou choro. III. Se choro, então não sorrio. IV. Não sinto fome ou grito. A partir dessas afirmações, […]
(VUNESP – TCE/SP – 2017 – Agente da Fiscalização) Se a afirmação “Ou Renato é o gerente da loja ou Rodrigo é o dono da loja” é verdadeira, então uma afirmação necessariamente verdadeira é: a) Renato é o gerente da loja e Rodrigo é o dono da loja. b) Renato […]
(VUNESP 2010 – Analista – Economia) Em uma sociedade, há 20% de pobres. Os negros são 50% da população, porém, são 80% dos pobres. Qual o percentual de pobres entre os negros? a) 32%. b) 40%. c) 50%. d) 60%. e) 80%. Solução: Gabarito: […]
VUNESP 2014 – FUNDESP – Analista de redes pleno Considere verdadeiras as premissas I, II e III. Se Cláudio é médico, então Ana é advogada. Se Marcelo é professor, então Débora é dentista. Ana não é advogada ou Débora não é dentista. A alternativa que contém uma conclusão que pode […]
(UFMG 2010 – Assistente de Administração) Considere as premissas: • Andrea não é loira ou Paula é alta. • Paula não é alta ou Carla é baixa. • Paula é alta ou Carla é baixa ou Andrea é loira. • Andrea é loira ou Carla não é baixa. A partir […]
(TCE/SP – 2015 / FCC) Considere verdadeiras as afirmações: − Daniel não bebe cerveja. − Se André prefere doces, então Bernardo bebe água. − Se Caio gosta de feijoada, então Daniel bebe cerveja. − Bernardo bebe água ou Caio gosta de feijoada. A partir dessas afirmações é possível concluir, corretamente, […]
(PREF. DE GOIANIA – Auditor de Tributos – CSUFG/2016) Considere verdadeira a informação “se a empresa A dobrar seu capital então a empresa B vai triplicar o seu capital”, e falsa a informação “a empresa A vai dobrar o seu capital e a empresa B vai triplicar seu capital”. Nessas […]
IV – Quantidade de linhas das tabelas verdade Uma questão que é, frequentemente, levantada quando se trabalha com tabelas verdade, é a partir de um determinado número de proposições simples que compõe uma função lógica, qual será a quantidade, máxima, de linhas da tabela verdade de tal função lógica. Podem […]
III – Tabela verdade dos conectivos lógicos Conjunção (e): A conjunção de duas sentenças e , escritas na forma de lógica proposicional como , será verdadeira se ambas, e , forem verdadeiras, e será falsa se ou for falsa ou se ambas forem falsas. O significado do operador “” pode […]
II – Proposições compostas e conectivos lógicos As proposições são, geralmente, simbolizadas por letras do alfabeto. Faremos aqui o uso das letras e para simbolizar proposições, no entanto, pode-se fazer uso de qualquer letra. : Brasília é a capital do Brasil. : Moscou é a capital da França. As duas […]
Os números , e são positivos inteiros. Uma maçã custa , uma banana custa , e uma cereja custa . O custo de maçãs, bananas, e cerejas é de . Qual deve ser o custo de uma maçã, duas bananas e uma cereja? Esse problema fez parte das […]
Como o nome sugere, lógica proposicional é um ramo da lógica matemática que estuda as relações lógicas entre proposições (ou declarações, sentenças, e afirmações) tomadas como um todo, e via conectivos lógicos. A lógica proposicional é também conhecida pelos nomes lógica sentencial, cálculo proposicional e cálculo sentencial. É importante em uma variedade de campos, […]
Problema aplicado no exame nacional de matemática e estatística do governo Neozelandês gera polêmica e ganha destaque na mídia internacional com repercussão nos principais jornais da Austrália, Reino Unido e Estados Unidos. O exame ocorreu em novembro de 2017, e uma das questões que ganhou notoriedade faz parte da prova […]
Segundo o autor britânico Simon Lehna Singh em seu livro de 1997 entitulado “O Último Teorema de Fermat” e que dirigiu o premiado documentário da BBC de mesmo nome, este teorema foi “o enigma que confundiu as maiores mentes do mundo durante 358 anos” ou segundo o prefaciador, dessa mesma […]
O determinante é a soma dos produtos dos elementos de uma fila pelos respectivos adjuntos.” Antes de desenvolver o teorema, vamos recordar a definição de e , além de um teorema particular. Chama-se Determinante Menor relativo a um elemento da matriz quadrada, o determinante que se obtém, suprimindo a lina […]
Uma forma de se obter o Logaritmo Natural de um número no escopo dos Reais em condições estabelecidas, é através da identidade (1) na condição . Exemplo: Calcular . Solução: Usando a identidade acima, isto é, a função escrita por uma série de potências, única, e em particular , temos: […]
Discussão da integral (1) A solução para a integral acima (1) não é obvia, a estratégia a ser utilizada, será multiplicar e dividir esta expressão por , (2) A partir daqui, o caminho é fazer uma substituição de variáveis, no caso, deve-se considerar nesta substituição (3) cuja […]
Discussão da integral (1) A solução para a integral acima (1) não é obvia, a estratégia a ser utilizada, será multiplicar e dividir esta expressão por , (2) A partir daqui, o caminho é fazer uma substituição de variáveis, no caso, deve-se considerar nesta substituição (3) cuja […]